�����o�ߕ���031007���@����
����҂̉h�{���z�ɂ���ԓI�َ����F��H�ґ��l���ւ̕ߐH�҂̖���
"Spatial
heterogeneity induced by consumers' nutrient
recycling:**
A new perspective in prey diversity."
** ���X�Ȃ����hSpatial heterogeneity by consumer-driven nutrient recycling:~�h �̕����Ȍ���������������Ȃ�
�v�|
�v�����N�g���̃p���h�N�X�ɂ��Đ������闝�_�̂ЂƂƂ��āA�n�̋�ԓI�ȕs�ψꐫ���d�v�ł���Ƃ����Ă���B
�{�����ł͌n�̕s�ψꐫ�����v���Ƃ��ē����v�����N�g���̔r�o�ɒ��ڂ��A�ߐH�҂ɂ��h�{�����T�C�N�������Y�҂̑��틤���𑣂��v���ƂȂ肤�邱�Ƃ��������B
Introduction
l Stoichiometory����݂����ނ̎��������`�v�����N�g���̃p���h�N�X
Ø �����n�ɋ��������e�����̔䗦�Ƌ����킲�ƂɎ������p�䗦���قȂ�
���ł����p�����������킪���̌n�ɂ����čœK�Ȏ�ƂȂ�B
Ø 2��ނ̎������߂��鑽�푔�ނ̋�����Stoichiometory
���݂��Ɍ݂��̗����ƂȂ鎑���̗��p�ɑ�z���Ă���2�킪�����ł���B(Tilman, 1982)
Ø ��O�ł͎������ȏ�̑��틤�����������Ă���(�悤�Ɍ�����)�B
l �ߐH�҂ɂ��h�{���ďz��(Consumer-driven Nutrient Recycle=CNR)�Ƒ��ނ̎�������
Ø �G�T�����e�����̔䗦�ƕߐH�҂̎������p�䗦���قȂ�
���ߐH�҂͗]�蕪�̎��������T�C�N������B
Ø 2��ނ̎������߂��鑔�ނ̋�����CNR
����ԓI�ɋψ�Ȍn�ł́ACNR�ɂ���ċ�������鎑���䗦���ɒ[�ɕ邽�ߑ��ނ̈��苤���͍���ɂȂ�B(Andersen, 1997)
l �v�����N�g���̃p���h�N�X��������郁�J�j�Y���`�n�̋�ԓI�َ������d�v
Ø ����҂͎킲�ƂɍD�K�Ȏ����v���䂪�قȂ邽�߁A���������䂪��ԓI�ɈقȂ�Α���̋���������ł���B(Tilman, 1982)
l �ߐH�҂ɂ��h�{���ďz��(CNR)�Ƒ��ނ̎�������
Ø �ߐH�҂���ԓI�ɕs�ψ�ɑ��݂���Ƃ��ACNR�̌��ʂ̋�ԓI�ȈႢ�ɂ���Ď����̋�ԓI�ȕs�ψꐫ���o����
�����F�ߐH�҂ɂ��h�{���ďz�ɂ��Ă̋�ԍ\�����l������ƁA���ނ̑��틤���͑��i�����̂ł͂Ȃ���?
�����ŁA�ߐH�ҌQ�W�̋�ԍ\��(�Ǎݐ�)���l������3�h�{�i�K�̃P���X�^�b�g���f�����l���A�V�~�����[�V�������f����p���đ��ނ̋����ɂ��ĕߐH�ҥ�g�U������ʂ��ǂ̂悤�ɉe�����邩�ɂ��Ē��ׂ�B
���f��
l ����Ԍn
���̊i�q��ԏ�ŁA�i�q�Ԃ��v�����N�g�����ړ������ނƉh�{�����g�U���郂�f����p���āA�ߐH�҂̈ړ����Ɗg�U�W���̈Ⴂ�ɂ�鑔�ނ̋����퐔�̕ω�������B
l �ߐH�҂̉h�{�����T�C�N��
�ߐH�҂̐����ɗ��p����Ȃ������h�{���́A���ނ��������p�ł���`�Ŕr�o�����Ɖ��肵���B
l �����v�����N�g���ɂ��Ă̌̃x�[�X���f��
�����v�����N�g���̊i�q�Ԃ̈ړ����������߁A�����v�����N�g���̓��Ԃ��̃x�[�X���f���ŋL�q�����B
l ���ނ̋����\�͂�trade-off
���ނ̋����\�͂ɂ��āA�̓��̒��f�ܗL���ƃ����ܗL���̉����l�ɐ��`��trade-off�����肵���B
l �x�[�X�ƂȂ郂�f���̏ڍׂɂ��Ă͕ʎ�[���f���̊T�v]���Q��
����
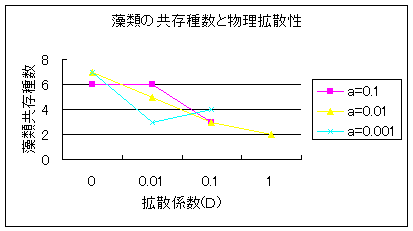
l ����҃��T�C�N���n�ł̋�ԍ\���͐��Y�҂̑��틤���̑��i�ɂȂ�炵���B
l �n�̕����I�Ȋg�U���͒Ⴍ�Ȃ���Ȃ�Ȃ�
l �����v�����N�g���̈ړ����͒Ⴍ�Ȃ���Ȃ�Ȃ��c�H
l �h�{���̋��������̈Ⴂ(������)�ɂ��Ă͂܂��s���B
ToDO
l �h�{�������Ȃǂ̊e�������ς����f�[�^���ł��邾������������B

���f���� ��031007��
�����v�����N�g��1��A���ނ���A�h�{��2��̂R�w�h�{�i�K�̃��f���͉E�}�̂悤�ȎO�w�\���̃��f���ŕ\�������B�{���f���ł͕����z�Ƃ��āA���ނɂ��h�{���̎�荞�݁A�ߐH�҂ɂ�鑔�ނ̕ߐH�A�ߐH�҂���̉h�{���̔r�o��z�肵�Ă���B
�ȉ��ł͊e�h�{�i�K���Ƃ̓��Ԃɂ��Ă̎����L�q����B
�P�DZooplankton
�P�D�ߐH�҂�����̃o�C�I�}�X����
�@�ߐH�҂ł��铮���v�����N�g���̒P�ʂ�����̃o�C�I�}�X�iZ�j�̓��Ԃ́A�����̐���(g)�Ǝ��S��(M)����ȉ��̂悤�ɗ^����B
![]()
�����̐���(g)�͓�����(I)�Ɠ�������(e)�ƌċz�ɂ�鑹��(r)�̊��Ƃ��A�����ƂȂ�h�{���ɂ���ė�����������(FR)���l����B
![]()
![]()
![]()
�����ʂ͍ő哯���ʁiImax�j�Ɖa�Z�x(FC)�̖O�a�a�Z�x(FC,max)�ɑ��銄���̐ςŗ^�����A�a�Z�x(FC)�͑��ނ��ւ̕ߐH��(aiAi)�̑��a�ŗ^������B�܂��h�{���ɂ�闥��(FR)��Liebig�̍ŏ����̌`�ŋL�q���A�a��(C)�Ɖa�̎�(QR)�A�����ɂ��h�{���̗v����(��R)�ŗ^����B
�����v�����N�g���͑��ނ̗��p�\�Ȏ����Ƃ��Ĕr�o����Ƒz�肵�āA�����v�����N�g���̉h�{���r�o��(��R)�͓���������(IQR)�Ɛ����ɗ��p�����h�{����(g��R)��p���Ĉȉ��̎��ŗ^������B
![]()
�Q�D�ߐH�Ҍ̐��̓���
�����v�����N�g���̌̐��̓��Ԃɂ��Č̃x�[�X���f���Ƃ��ċL�q����B����i�q�ɂ�����̐�(n)�̓��Ԃ́A�ȉ��̂悤�ɗ^������B
![]()
��P���͊e�̂̐��Y���闑�̑��a(��b)�A��Q���͌̂̎��S��(M)�A��R���͈ڏo��(m)�ɂ����̊g�U�ʂł���B�����v�����N�g����j�����Y���闑��(bj)�́A�����v�����N�g���̏����Y��(Zj - Z*)�Ɨ��T�C�Y(E)��p���Ĉȉ��̎��ŗ^������B
![]()
�Q�DAlgae
���ރo�C�I�}�X�̓��Ԃ͈ȉ��̎��ŗ^����B��P���͐�����(��)�Ɣ�H�ȊO�̑�����(d)�Ɗ�ߗ�(D)�A��Q���͔�H��(IiZ)�A�R���œ��̊g�U�ʂ�^���Ă���B
![]()
��H��(IiZ)�͉a�Ƃ��ĕߐH���ꂽ�����̑���Ai����߂�ʂł���B
![]()
��������i (day-1) �͐����ƂȂ�h�{���ɂ���ė�������A�h�{���ܗL���Ɖa�̉h�{���ʂ���L�q�����B
![]()

![]()

�R�DResource (Nutrient)
�n������(R)�̓��Ԃ͈ȉ��̎��ɂ��L�q�����B
![]()
��P���͗����o�A��Q���͑��ނ̋z���ʂ̑��a�A��R���͓����̔r�o��(��Z)�A��S���͓��̊g�U�ʂ�^���Ă���B
�S�DParameter Settings
�� ���ނ̌`���l�F�ŏ��ܗL���̒��f�|�����Ԃ�trade-off
���ނ̉h�{���z�����x�����߂�p�����[�^�l�ɂ��āA�����I�Ȍ������̂��߂ɁA���ނ̉h�{���̋z���e�a���ɂ��đ��ލזE���\�ʏ�̉h�{����荞�݃`�����l�������L���ƍl���Đ��`��trade-off��z�肵���i����͍זE���̕\�ʐς��L���ƍl���Ă������ł���j�B�قȂ鎑���Ԃ̃g���[�h�I�t���f���̐����I���J�j�Y������̐����́AMuller et al. (2001), Ecol. Letters(2001), 4, pp519-529 ����сAKoijman(2000), Cambridge Univ. press(2000)�ɏڂ����B
���f�ƃ����̈�זE������̍ő�z�����xVN,max�CVP,max�́A���f�ƃ����߂��閌��`���l���i�������͌����T�C�g�j�̐�����N�C��P�Ƃ��A��̃`���l���̍ő�̓��ߐ��i�e�a���j�����fN�C���fP�Ƃ���ƈȉ��̎��ŗ^������B
![]()
![]()
�����ŁA����̃`�����l���̑��a�i��N+nP�j�����Ɖ��肵�ď㎮��ό`����ƈȉ��̎����������B
![]() �@[C�͒萔]
�@[C�͒萔]
����ɁA����̃`�����l���̍ő哧�ߐ����fR������łقړ����ł���ƍl������̂Ń��fN/���fP�͒萔(>�P)�ł���B����đ��ގ�i�̒��f�ƃ����̍ő�z�����x�͐��`��trade-off�����肵���ȉ��̊W���ŗ^������B
![]() �@[K,C�͒萔]
�@[K,C�͒萔]
���ނ��\����carbon-rich�ł���Ƃ��ɂ͍ő�h�{���z�����xVR,max���h�{���̍ŏ��ܗL��QR,min�ɂقڔ�Ⴗ��ƍl����ƈȉ��̎������藧�B
![]()
���������čŏ����f�ܗL��QN,min�ƍŏ������ܗL��QP,min�̊W�͐��`��trade-off�ŋߎ��ł���B
![]() �@[K�f,C�f�͒萔]
�@[K�f,C�f�͒萔]
Notation: List of Parameters.
Symbol |
Definition |
Units |
Notes or Assigned value |
|
Indices: |
|
|
|
|
i |
Index for algae species |
|
|
|
R |
Index for resources (N, P) |
|
|
|
x |
spatial dimension |
|
|
|
y |
spatial dimension |
|
|
|
|
|
|
|
|
State Variables: |
|
|
|
|
Ai |
Biomass of i-th algae |
�ʂ� (C) litter-1 |
|
|
n |
Number of zooplankton individuals |
|
|
|
Z |
Biomass of zooplankton individual |
�ʂ� (C) liter-1 |
|
|
SR |
Concentration of dissolved nutrient R |
�ʂ� (R) litter-1 |
|
|
|
|
|
|
|
Functions: |
|
|
|
|
b |
Hatch number of zooplankton |
|
|
|
g |
Per capita growth rate for zooplankton |
d-1 |
|
|
FC |
Available algal biomass for zooplankton |
�ʂ� (C) litter-1 |
|
|
FR |
Liebig coefficient of nutrient R (N, P) for zooplankton |
d-1 |
from 0 to1 |
|
��R |
�����v�����N�g���̉h�{��R�̔r�o�� |
�ʂ� (R) liter-1 d-1 |
|
|
|
|
|
|
|
��i |
Per capita reproductive rate for i-th algae |
d-1 |
|
|
I |
Assimilation efficiency for algae by zooplankton |
�ʂ� (C) liter-1 d-1 |
|
|
QR,i |
Quota of nutrient R for i-th algae |
�ʂ� (R) liter-1 |
|
|
VR,i |
Net uptake of nutrient R for i-th algae |
�ʂ� (R) liter-1 d-1 |
|
|
|
|
|
|
|
Parameters: |
|
|
|
|
e |
Ingestion rate for zooplankton |
Dimensionlessfv |
|
|
FC,max |
�O�a�a�Z�x |
�ʂ� (C) litter-1 |
|
|
Imax |
Maximal assimilation efficiency for algae by zooplankton |
�ʂ� (C) liter-1 d-1 |
���O�a�a�Z�x�̂Ƃ��̉a������ |
|
r |
Coefficient for maintenance-related algal respiration |
d-1 |
|
|
��R |
Quota of nutrient R for zooplankton |
�ʂ� (R) liter-1 |
|
|
m |
Migration rate for zooplankton individual |
d-1 |
|
|
M |
Mortality rate for zooplankton individual |
d-1 |
|
|
Z* |
threshold biomass to lay egg for zooplancton individual |
�ʂ� (C) liter-1 |
|
|
E |
���������̒Y�f�� |
�ʂ� (C) liter-1 |
|
|
|
|
|
|
|
��R,max,i |
Maximal reproductive rate restricted by nutrient R for i-th algae |
d-1 |
|
|
ai |
Attack rate of zooplankton on i-th algae |
m3 liter-1 d-1 |
|
|
di |
Per capita mortality rate for i-th algae |
d-1 |
|
|
QR,max,i |
Maximal quota of nutrient R for i-th algae |
�ʂ� (R) litter-1 |
|
|
QR,min,i |
Minimal quota of nutrient R for i-th algae |
�ʂ� (R) litter-1 |
|
|
VR,max,i |
Max net uptake of nutrient R for i-th algae |
�ʂ� (R) liter-1 |
|
|
��i |
Dispersal ratio for i-th algae |
d-1 |
|
|
|
|
d-1 |
|
|
D |
Dilution rate for chemostat system |
d-1 |
|
|
SR,in |
Supply concentration for nutrient R |
�ʂ� (R) litter-1 |
|
|
��R |
Dispersal ratio for nutrient R |
d-1 |
|
|
|
|
|
|
